231x Filetype PDF File size 0.05 MB Source: users.math.msu.edu
Math 110 Lecture #19
CH. 4.3-4.4 (PART I). Logarithmic Function. Logarithmic equations.
Change-of-Base Formula.
For any logarithmic bases a and b, and any
positive number M,
log M=logaM
b log b
a
Problem #1.
Use your calculator to find the following logarithms.
Show your work with Change-of-Base Formula.
log 10 log 9 log 11
a) b) c)
2 1 7
3
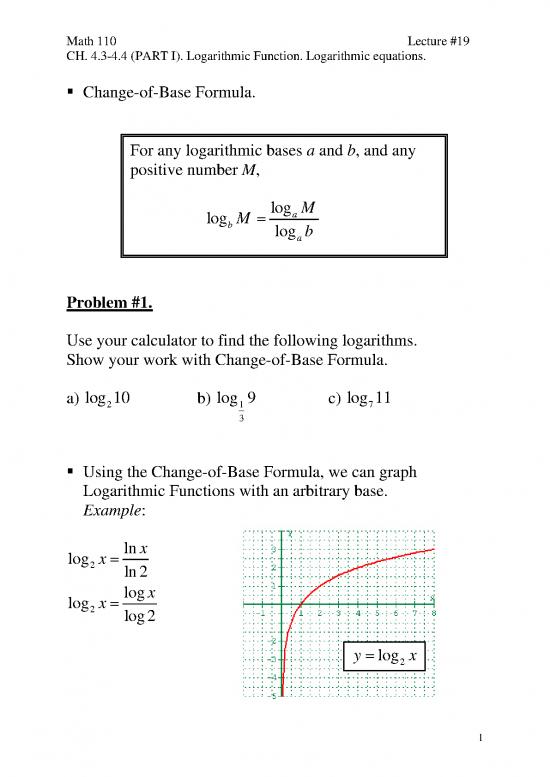
Using the Change-of-Base Formula, we can graph
Logarithmic Functions with an arbitrary base.
Example:
log x = ln x
2 ln2
logx
log2 x = log2
y = log2 x
1
Math 110 Lecture #19
CH. 4.3-4.4 (PART I). Logarithmic Function. Logarithmic equations.
Properties of Logarithms.
If b, M, and N are positive real numbers, b ≠1, p, x are real
numbers, then
1. log MNM=+log log N
product rule
bbb
2. log M =−log M log N quotient rule
bbb
N
log Mp = plog M
3. power rule
bb
⎧ x
4. ⎪logbbx= inverse property of logarithms
⎨ log x
b
bx=>,0x
⎪
⎩
5. log M ==log N if and only if M N
bb .
This property is the base for solving Logarithmic
Equations in form log gx=log hx.
( ) ( )
bb
Properties 1-3 may be used for Expanding and Condensing
Logarithmic expressions.
Expanding and Condensing Logarithmic expressions.
2
Math 110 Lecture #19
CH. 4.3-4.4 (PART I). Logarithmic Function. Logarithmic equations.
Problem #2.
Express each of the following expressions as a single
logarithm
whose coefficient is equal to 1.
a) 1⎡⎤
++ −−
3log xx1 2log 3 log7
()()
5⎣⎦
11
⎡⎤
++ −+
b) ln xx1 2ln 1 ln x
()()
⎣⎦
23
11
⎡⎤
c) +− + +
ln xx3 ln 3ln x1
() ()
⎣⎦
25
1⎡⎤
−+ +−
d) log xx2 2log 2 log5
()()
2⎣⎦
Problem #3.
Expand a much as possible each of the following.
x2y
a) log z5
x3y
b) ln 4
z3
Solving Logarithmic Equations.
3
Math 110 Lecture #19
CH. 4.3-4.4 (PART I). Logarithmic Function. Logarithmic equations.
1. Solving the Simplest Logarithmic Equation (SLE).
Given: log xa= a
b , b > 0, b ≠1, is any real number.
According the definition of the logarithm this equation is
equivalent to x = ba.
2. According to properties of logarithms, if
log M = log N , then M = N.
bb
Remember, check is part of solution for
Logarithmic Equations.
Problem #4. Solve the following Logarithmic Equations.
a) log2 x =5
b)
log x−=25
3 ()
c) 2
log xx−=log6
()
d)
log x+=4 −3
1 ()
2
4
no reviews yet
Please Login to review.