Authentication
470x Tipe PDF Ukuran file 0.21 MB
17. SOAL-SOAL PROGRAM LINEAR
daerah 5x + y ≥ 10 berada pada garis persamaan tersebut
dan di atas garis (I, II,III, V) ---(a)
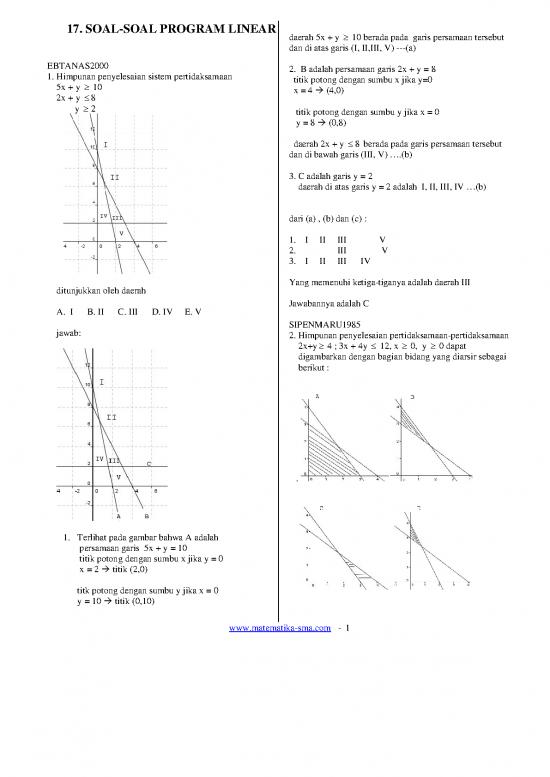
EBTANAS2000
1. Himpunan penyelesaian sistem pertidaksamaan 2. B adalah persamaan garis 2x + y = 8
5x + y ≥ 10 titik potong dengan sumbu x jika y=0
2x + y ≤ 8 x = 4 Æ (4,0)
y ≥ 2
titik potong dengan sumbu y jika x = 0
y = 8 Æ (0,8)
daerah 2x + y ≤ 8 berada pada garis persamaan tersebut
dan di bawah garis (III, V) ….(b)
3. C adalah garis y = 2
daerah di atas garis y = 2 adalah I, II, III, IV …(b)
dari (a) , (b) dan (c) :
1. I II III V
2. III V
3. I II III IV
Yang memenuhi ketiga-tiganya adalah daerah III
ditunjukkan oleh daerah
Jawabannya adalah C
A. I B. II C. III D. IV E. V
SIPENMARU1985
jawab: 2. Himpunan penyelesaian pertidaksamaan-pertidaksamaan
2x+y≥ 4 ; 3x + 4y ≤ 12, x ≥ 0, y ≥ 0 dapat
digambarkan dengan bagian bidang yang diarsir sebagai
berikut :
.
1. Terlihat pada gambar bahwa A adalah
persamaan garis 5x + y = 10
titik potong dengan sumbu x jika y = 0
x = 2 Æ titik (2,0)
titk potong dengan sumbu y jika x = 0
y = 10 Æ titik (0,10)
www.matematika-sma.com - 1
Jawab :
2x+y≥ 4 ;
2x + y = 4
titik potong dengan sumbu x , y = 0
x = 2 Æ (2,0) Jawabannya adalah E
titik potong dengan sumbu y, x = 0 UN2005 SMK
y = 4 Æ (0,4) 3. Daerah yang diarsir merupakan himpunan penyelesaian
dari sistem pertidaksamaan linear…
3x + 4y ≤ 12
3x + 4y = 12
titik potong dengan sumbu x, y = 0
x = 4 Æ (4,0)
titik potong dengan sumbu y, x = 0
y=3 Æ (0,3)
gambar sbb:
A. x+2y≤8, 3x+2y≤12, x≥0, y≥0
B. x+2y≥8, 3x+2y≥12, x≥0, y≥0
C. x-2y≥8, 3x-2y≤12, x≥0, y≥0
D. x+2y≤8, 3x-2y≥12, x≥0, y≥0
E. x+2y≤8, 3x+2y≥12, x≥0, y≥0
Jawab :
persamaan garis melalui titik (0,6) dan (4,0) adalah:
(0,a) (b,0)
Persaman garis = x + y = 1 ⇔ ax + by = a.b
Himpunan penyelesaiannya berada di atas persamaan garis b a
2x + y = 4 dan di bawah 3x + 4y = 12
6x+4y = 24
⇔ 3x + 2y = 12
karena daerah arsiran dibawah persamaan garis maka
3x + 2y ≤ 12 …(1)
www.matematika-sma.com - 2
persamaan garis melalui titik (0,4) dan (8,0) adalah: Jawab:
1. persamaan garis melalui titik (0,6) dan (10,0) adalah:
(0,a) (b,0)
Persaman garis = x + y = 1 ⇔ ax + by = a.b (0,a) (b,0)
b a
ax + by = a.b ⇒ 6x + 10y = 60
4x+8y = 32 3x + 5y = 30
⇔ x + 2y = 8
karena daerah arsiran dibawah persamaan garis maka
karena daerah arsiran dibawah persamaan garis maka 3x + 5y ≤ 30 ….(1)
x + 2y ≤ 8 ….(2)
Arsiran di atas sumbu x dan di kanan sumbu y 2. persamaan garis melalui titik (0,-4) dan (2,0) adalah:
maka x≥0 dan y≥0 ….(3) dan (4)
sehingga daerah penyelesaiannya adalah: (0,a) (b,0)
(1), (2), (3) dan (4)
ax + by = a.b ⇒ -4x + 2y = -8
3x + 2y ≤ 12, x + 2y ≤ 8 dan x≥0, y≥0 -2x + y = -4
jawabannya adalah A karena daerah arsiran di sebelah kiri maka persamaan
garisnya :
EBTANAS2001 SMK Teknologi -2x + y ≥ -4 atau 2x – y ≤ 4 …(2)
4. Daerah yang diarsir pada gambar di bawah adalah
himpunan penyelesaian dari sistem pertidaksamaan…
ingat untuk a < 0 dan b > 0
-ax + by ≥ -ab
(b,0)
x
(0,-a) -ax + by≤ -ab
y
3. Arsiran di atas sumbu x dan di kanan sumbu y
maka x≥0 dan y≥0 ….(3) dan (4)
A. 5x + 3y≤30, x - 2y≥4, x≥0, y≥0
B. 5x + 3y≤30, x - 2y≤4, x≥0, y≥0 sehingga daerah penyelesaiannya adalah:
C. 3x + 5y ≤30, 2x - y≥4, x≥0, y≥0 (1), (2), (3) dan (4)
D. 3x + 5y≤30, 2x - y≤4, x≥0, y≥0
E. 3x + 5y≥30, 2x - y≤4, x≥0, y≥0 3x + 5y ≤ 30 ; 2x – y ≤ 4 ; x≥0 dan y≥0
jawabannya adalah D
www.matematika-sma.com - 3
SIPENMARU1985
5. Daerah yang diarsir pda gambar di bawah ini ax + by = a.b ⇒ 4x + 6y = 24
menunjukkan himpunan titik (x,y) yang memenuhi 2x + 3y = 12
pembatasan di bawah ini, yaitu ….
karena daerah arsiran di bawah persamaan
garis maka :
2x + 3y ≤ 12 …(2)
3. Arsiran di atas sumbu x dan di kanan sumbu y
maka x≥0 dan y≥0 ….(3) dan (4)
sehingga daerah penyelesaiannya adalah:
(1), (2), (3) dan (4)
-x + y ≤2 ; 2x +3y ≤ 12 ; x≥0 dan y≥0
A. x≥0, y≥0, 2x + 3y≤12, - x + y≥ 2
B. x≥0, y≥0, 2x + 3y≥12, -x + y≥ 2 jawabannya adalah C
C. x≥0, y≥0, 2x + 3y ≤12, -x + y≤ 2
D. x≥0, y≥0, 2x + 3y≥12, -x + y≤ 2 EBTANAS1998
E. x≥0, y≥0, 2x + 3y≤12, -x + y≤ 2 6. Daerah yang diarsir pada gambar merupakan grafik
himpunan penyelesaian sistem pertidaksamaan…
jawab: y
1. persamaan garis melalui titik (0,2) dan (-2,0) adalah: B(3,6)
C(0,4)
(0,a) (b,0)
ax + by = a.b ⇒ 2x - 2y = -4
x - y = -2
A(7,0)
karena daerah arsiran di sebelah kanan persamaan garis
maka
x – y ≥ -2 atau –x + y ≤ 2….(1) A. 3x + 2y≤21, -2x +3y≤12, x≥0, y≥0
B. 2x + 3y≤21, -2x - 3y≤12, x≥0, y≥0
C. -3x +2y ≥21, -2x+3y≥12, x≥0, y≥0
untuk a > 0 dan b <0 D. -3x-2y≥21, 2x +3y≥12, x≥0, y≥0
E. 3x -2y≥21, 2x -3y≥12, x≥0, y≥0
y
jawab:
ax - by ≤ -ab (0,a) . Persamaan garis melalui titik (x1, y1) dan (x2 , y2 )
adalah:
ax - by ≥ -ab
y − y x−x
1 = 1
x y − y x −x
(-b,0) 2 1 2 1
1. persamaan garis melalui titik (0,4) dan (3,6)
2. persamaan garis melalui titik (0, 4) dan (6,0) adalah: (x1, y1) (x 2 , y 2 )
y − 4 = x − 0 ⇔ y − 4 = x
6−4 3−0 2 3
(0,a) (b,0)
www.matematika-sma.com - 4
no reviews yet
Please Login to review.