144x Filetype PDF File size 0.56 MB Source: www.pxu.org
Name__________________________
AP Calculus BC Summer Review Packet (Limits & Derivatives)
Limits
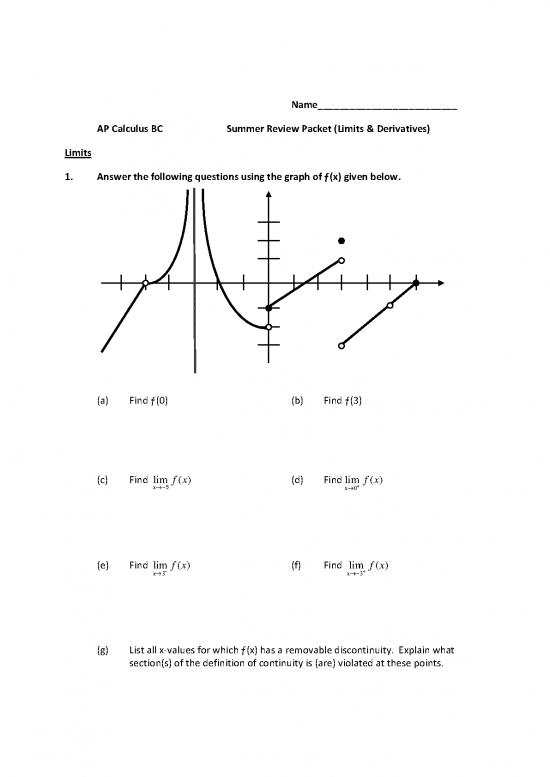
1. Answer the following questions using the graph of ƒ(x) given below.
(a) Find ƒ(0) (b) Find ƒ(3)
(c) Find (d) Find
lim fx( ) lim fx( )
x5 x0
(e) Find (f) Find
lim fx( ) lim fx( )
x3 x3
(g) List all x-values for which ƒ(x) has a removable discontinuity. Explain what
section(s) of the definition of continuity is (are) violated at these points.
(h) List all x-values for which ƒ(x) has a nonremovable discontinuity. Explain what
section(s) of the definition of continuity is (are) violated at these points.
In problems 2-10, find the limit (if it exists) using analytic methods (i.e. without using a
calculator).
2 1cos2 x
3xx21 30
2. lim 3 3. lim
x2 x 8 x/6 4x
1/(x1) 1
lim x31
4. 5. lim
x4 x4 x0 x
3
1/ 1x 1 sin6
6. lim 7. lim
x0 x 0 7
22 6x36
8. limsin 3t 9. lim
t0 t3 x6 6x
10. lim sin(( /6)x)(1/2)
x 0 x
Hint: sin( )sincos cossin
2x1 3,0x
11. Suppose fx() .
x1
2
4x k,x 0
(a) For what value of k will f be piecewise continuous at x = 0? Explain why this is
true using one-sided limits. (Hint: A function is continuous at
x =c if (1) f(c) exists, (2) exists, and (3) .)
lim fx( ) lim f (x) f (c)
xc xc
(b) Using the value of k that you found in part (a), accurately graph f below.
Approximate the value of
lim fx( )
x1
lim fx( ) _______________
x1
(c) Rationalize the numerator to find analytically.
lim fx( )
x1
no reviews yet
Please Login to review.