Filetype PDF | Posted on 25 Jan 2023 | 2 years ago
Authentication
digital resources
148x Filetype PDF File size 0.19 MB Source: www.csusm.edu
CALCULUS TRIGONOMETRICDERIVATIVESANDINTEGRALS
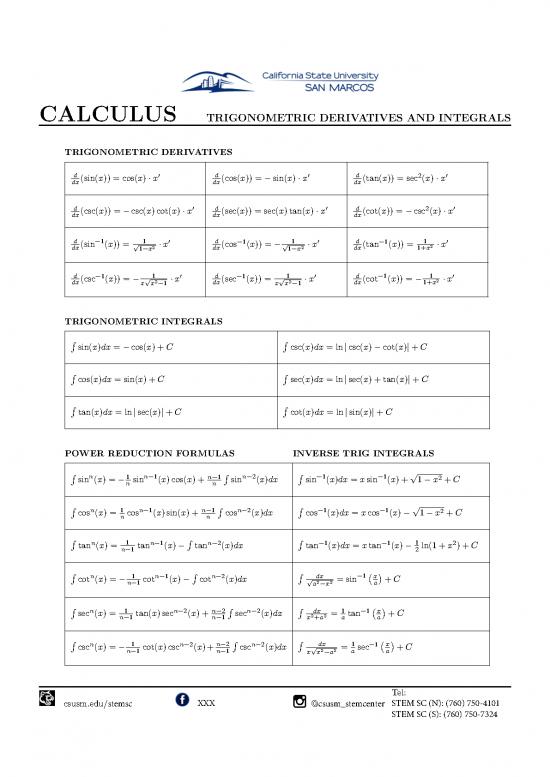
TRIGONOMETRICDERIVATIVES
d 0 d 0 d 2 0
dx(sin(x)) = cos(x) · x dx(cos(x)) = sin(x)·x dx(tan(x)) = sec (x)·x
d 0 d 0 d 2 0
dx(csc(x)) = csc(x)cot(x)·x dx(sec(x)) = sec(x)tan(x)·x dx(cot(x)) = csc (x)·x
d (sin 1(x)) = p 1 2 · x0 d (cos 1(x)) = p 1 2 ·x0 d (tan 1(x)) = 1 2 · x0
dx 1 x dx 1 x dx 1+x
d (csc 1(x)) = p1 · x0 d (sec 1(x)) = p1 · x0 d (cot 1(x)) = 1 · x0
dx x x2 1 dx x x2 1 dx 1+x2
TRIGONOMETRICINTEGRALS
R sin(x)dx = cos(x)+C R csc(x)dx =ln|csc(x) cot(x)|+C
R cos(x)dx =sin(x)+C R sec(x)dx =ln|sec(x)+tan(x)|+C
R tan(x)dx =ln|sec(x)|+C R cot(x)dx =ln|sin(x)|+C
POWERREDUCTIONFORMULAS INVERSE TRIG INTEGRALS
R sinn(x)= 1 sinn 1(x)cos(x)+n 1 R sinn 2(x)dx R sin 1(x)dx = xsin 1(x)+p1 x2 +C
n n
R cosn(x)=1 cosn 1(x)sin(x)+n 1 R cosn 2(x)dx R cos 1(x)dx = xcos 1(x) p1 x2 +C
n n
R tann(x)= 1 tann 1(x) R tann 2(x)dx R tan 1(x)dx = xtan 1(x) 1 ln(1+x2)+C
n 1 2
R n 1 n 1 R n 2 R p dx 1 x
cot (x)= n 1cot (x) cot (x)dx a2 x2 =sin a +C
R n 1 n 2 n 2 R n 2 R dx 1 1 x
sec (x)=n 1 tan(x)sec (x)+n 1 sec (x)dx x2+a2 = a tan a +C
R n 1 n 2 n 2 R n 2 R pdx 1 1 x
csc (x)= n 1cot(x)csc (x)+n 1 csc (x)dx x x2 a2 = a sec a +C
Tel:
csusm.edu/stemsc XXX @csusm_stemcenter STEM SC (N): (760) 750-4101
STEM SC (S): (760) 750-7324
CALCULUS TRIGONOMETRICDERIVATIVESANDINTEGRALS
STRATEGYFOREVALUATINGRsinm(x)cosn(x)dx
(a) If the power n of cosine is odd (n =2k +1), save one cosine factor and use cos2(x)=1 sin2(x)to
express the rest of the factors in terms of sine:
Z sinm n Z m 2k+1 Z m 2 k
(x)cos (x)dx = sin (x)cos (x)dx = sin (x)(cos (x)) cos(x)dx
Z m 2 k
= sin (x)(1 sin (x)) cos(x)dx
Then solve by u-substitution and let u =sin(x).
(b) If the power m of sine is odd (m =2k + 1), save one sine factor and use sin2(x)=1 cos2(x)to
express the rest of the factors in terms of cosine:
Z sinm n Z 2k+1 n Z 2 k n
(x)cos (x)dx = sin (x)cos (x)dx = (sin (x)) cos (x)sin(x)dx
=Z (1 cos2(x))kcosn(x)sin(x)dx
Then solve by u-substitution and let u = cos(x).
(b) If both powers m and n are even, use the half-angle identities:
sin2(x)=1(1 cos(2x)) cos2(x)=1(1+cos(2x))
2 2
R m n
STRATEGYFOREVALUATING tan (x)sec (x)dx
(a) If the power n of secant is even (n =2k,k 2), save one sec2(x) factor and use sec2(x) = 1+tan2(x)
to express the rest of the factors in terms of tangent:
Z m n Z m 2k Z m 2 k 1 2
tan (x)sec (x)dx = tan (x)sec (x)dx = tan (x)(sec ) sec (x)(x)dx
Z m 2 k 1 2
= tan (x)(1+tan (x)) sec (x)(x)dx
Then solve by u-substitution and let u = tan(x).
(b) If the power m of tangent is odd (m =2k + 1), save one sec(x)tan(x) factor and use tan2(x)=
sec2(x) 1 to express the rest of the factors in terms of secant:
Z tanm n Z 2k+1 n Z 2 k n 1
(x)sec (x)dx = tan (x)sec (x)dx = (tan (x)) sec (x)sec(x)tan(x)dx
=Z (sec2(x) 1)ksecn 1(x)sec(x)tan(x)dx
Then solve by u-substitution and let u =sec(x).
Tel:
csusm.edu/stemsc XXX @csusm_stemcenter
STEM SC (N): (760) 750-4101
STEM SC (S): (760) 750-7324
no reviews yet
Please Login to review.
