Filetype PDF | Posted on 25 Jan 2023 | 2 years ago
Authentication
digital resources
105x Filetype PDF File size 1.21 MB Source: topdrawer.aamt.edu.au
Circle geometry theorems
http://topdrawer.aamt.edu.au/Geometric-reasoning/Big-ideas/Circle-
geometry/Angle-and-chord-properties
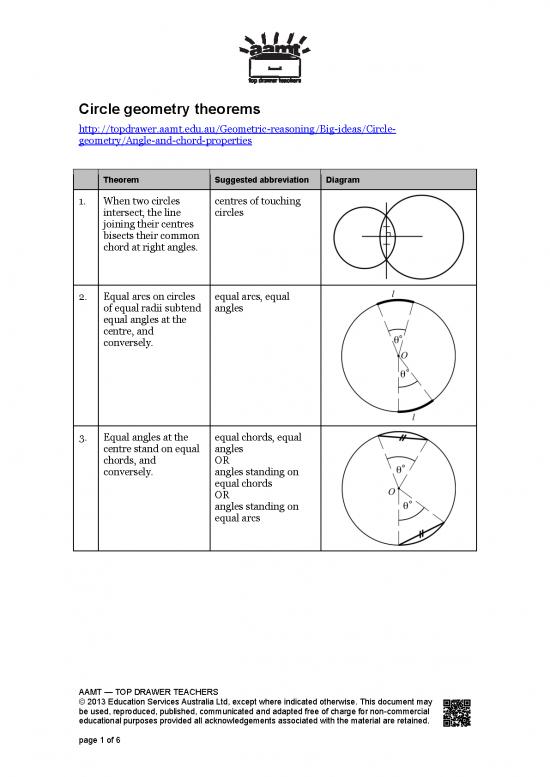
Theorem Suggested abbreviation Diagram
1. When two circles centres of touching
intersect, the line circles
joining their centres
bisects their common
chord at right angles.
2. Equal arcs on circles equal arcs, equal
of equal radii subtend angles
equal angles at the
centre, and
conversely.
3. Equal angles at the equal chords, equal
centre stand on equal angles
chords, and OR
conversely. angles standing on
equal chords
OR
angles standing on
equal arcs
AAMT — TOP DRAWER TEACHERS
© 2013 Education Services Australia Ltd, except where indicated otherwise. This document may
be used, reproduced, published, communicated and adapted free of charge for non-commercial
educational purposes provided all acknowledgements associated with the material are retained.
page 1 of 6
Theorem Suggested abbreviation Diagram
4. The angle at the angles at the centre
centre is twice the and circumference
angle at the
circumference
subtended b y the
same arc.
5. The tangent to a circle tangent perpendicular
is perpendicular to the to radius
radius drawn to t he
point of contact and
conversely.
6. The perpendicular perpendicular from
from the centre of a the centre
circle to a chord
bisects the chord.
7. The line from the line joining centre to
centre of a circle to midpoint of chord
the midpoint of a
chord is perpendicular
to the chord.
8. The perpendicular perpendicular
bisector of a chord bisector of
passes through the chord
centre of the circle.
AAMT — TOP DRAWER TEACHERS
page 2 of 6
Theorem Suggested abbreviation Diagram
9. Equal chords in equal equal chords
circles are equidistant equidistant from
from the centres. centre
10. Chords in a circle equal chords
which are equidistant equidistant from
from the centre are centre
equal.
11. Any three non- perpendicular
collinear points lie on bisector of chord
a unique circle, whose passes through the
centre is the point of centre
concurrency of the
perpendicular
bisectors of the
intervals joining the
points.
12. Angles in the same angles in the same
segment are equal. segment
13. The angle in a semi- angle in a semi-circle
circle is a right angle.
AAMT — TOP DRAWER TEACHERS
page 3 of 6
Theorem Suggested abbreviation Diagram
14. Opposite angles of a opposite angles in a
cyclic quadrilateral cyclic quad
are supplementary.
x + y = 180
15. The exterior angle at a exterior angle of cyclic
vertex of a cyclic quad
quadrilateral is equal
to the interior
opposite angle.
16. If the o pposite a ngles converse of opposite
in a quadrilateral are angles in a cyclic quad
supplementary then
the quadrilateral is
cyclic.
Note: This theorem is
also a test for four
points to be concyclic.
If x + y = 180 then ABCD is a
cyclic quadrilateral.
17. The products of the intersecting chords
intercepts of t wo
intersecting chords
are equal.
AP × BP = CP × DP
AAMT — TOP DRAWER TEACHERS
page 4 of 6
no reviews yet
Please Login to review.
